جمعه 25 مهر 1399 کد خبر: 37
۱- مقدمه
در مقاله قبل ناتواناییهای فیزیک کلاسیک و پدیدههایی که فیزیک کلاسیک قادر به توجیه آن نبود ذکر شد. خاصیت دوگانگی موجی-ذرهای اجسام مشاهده شد و آزمایشهای نشان دهنده هرکدام از آنها معرفی شد. در ادامه ابتدا به این سوال پرداخته میشود که چرا گسستگی انرژی و خاصیت موجی-ذرهای در ابعاد بزرگ ملموس نیست؟ همچنین به معادلات شرودینگر و اصل عدم قطعیت هایزنبرگ و نتایج آنها پرداخته میشود.
۲- چرا گسستگی انرژی و دوگانگی موجی ذرهای اجسام در ابعاد بزرگ ملموس نیست؟
همانطور که مشاهده شد، انرژی پیوسته نیست و گسسته است. همچنین برای اجسام خاصیت دوگانگی موجی-ذرهای مشاهده شد. این خواص به عنوان یک سری خواص کلی معرفی شدند، یعنی برای تمام مواد صدق میکنند. این به این معنی است که برای مثال خاصیت دوگانگی موجی-ذرهای برای ما نیز باید صدق کند. همچنین انرژی جنبشی یک دونده نیز باید گسسته باشد. اما مشاهده میشود که این گسستگی انرژی یا خاصیت دوگانگی موجی ذرهای به صورت ملموس دیده نمیشود. در ادامه دلیل این امر ذکر میشود.
۱-۲- گسستگی انرژی
برای بررسی گسستگی انرژی، انرژی یک فنر بررسی میشود. اگر فرض شود فنری با دامنه ۱۰ سانتیمتر کشیده شود، فرکانس آن در حدود ۰/۵۰۳ هرتز و انرژی آن در حدود ۰/۰۱۵ ژول بدست میآید. همانطور که توضیح داده شد، میزان گسستگی انرژی به اندازه hν میتواند باشد. باتوجه به مقدار بدست آمده برای فرکانس، میزان گسستگی انرژی برای این فنر مقداری برابر با ۳۴-۱۰ ژول بدست میآید. این مقدار بسیار بسیار کوچک است و در واقع دستگاهی وجود ندارد که این مقدار ناچیز انرژی را نشان بدهد. در نتیجه مشاهده میشود که درست است که گسستگی انرژی برای انرژی یک فنر هم صدق میکند اما میزان گسستگی انرژی برای آن بسیار بسیار کم است و به دلیل ناچیز بودن آن است که انرژی در این مقیاسها پیوسته فرض میشود. اما این میزان گسستگی انرژی (۳۴-۱۰ ژول) برای مثال برای الکترونها که انرژیهای بسیار کوچکی دارند قابل توجه میشود و در آن مقیاس گسستگی انرژی به صورت ملموس خود را نشان میدهد. انرژی الکترونها در محدوده الکترون ولت است که برابر با ۱۹-۱۰× ۱/۶ ژول میباشد و بسیار کمتر از انرژی است که برای مثال فنر بررسی شد.
۲-۲- دوگانگی موجی-ذرهای اجسام
همانطور که گفته شد تمام اجسام خاصیت دوگانگی موجی-ذرهای را از خود نشان میدهند. یعنی یک انسان نیز کاملا ذره نیست و خاصیت موجی از خود نشان میدهد. اما همانطور که میدانید این خاصیت موجی به صورت ملموس دیده نمیشود. برای مثال اگر طولموج یک انسان که در حال دویدن با سرعت عادی است حساب شود، مقداری با مرتبه بزرگی ۳۴- متر بدست میآید. دوباره مشاهده میشود که این مقدار بسیار کوچک است و عملا تکرار آن انسان (به عنوان یک موج) روی خودش میافتد و درنتیجه خاصیت موجی آن به صورت ملموس دیده نمیشود. اما اگر طولموج برای یک الکترون درون یک ساختار بلوری محاسبه شود مقدار حدودی یک آنگستروم بدست میآید. این مقدار برابر با فاصله بین اتمها در ساختار بلوری است. در نتیجه برای الکترون که طولموج آن در حد و اندازه فاصله صفحات بلوری (یعنی جایی که در آن حضور دارد) است خاصیت موجی به صورت ملموس دیده میشود. ولی برای یک انسان طولموج بدست آمده بسیار بسیار کوچکتر از اندازه فضایی است که در آنجا قرار دارد و به همین دلیل است که خاصیت موجی آن به صورت ملموس دیده نمیشود.
البته توضیح داده نشد که چگونه میتوان برای انسان یا سایر ذرات طولموج محاسبه کرد. این محاسبه به کمک رابطه دوبروی که در زیر نوشته شده است انجام میشود.
|
معادله۱ |
در این رابطه P بیانگر تکانه (حاصلضرب جرم در سرعت)، h بیانگر ثابت پلانک و بیانگر طولموج است. این رابطه کمک میکند که برای یک ذره با تکانه P، طولموج بدست آید و همچنین برای یک موج، با طولموج ، تکانه (به عنوان نمایندهای از خاصیت ذره جرمدار) بدست آید و عملا پلی است برای تبدیل خاصیت موجی به ذرهای و برعکس [۱-۳].
۳- معادله شرودینگر
در فیزیک کوانتوم برای اینکه بفهمیم که هر ذره در هر لحظه t درچه مکانی با مختصات X,Y,Z است از تابع موج استفاده میکنیم. حال معادله شرودینگر به ما میگوید که اگر ذرهای دارای انرژی E و پتانسیل V باشد، تابع موج آن چقدراست و انرژی و احتمال حضور الکترون به چه صورت است (در شرایط تعیین شده). این بیان سادهای بود از معادله شرودینگر و نتیجهای که در اثر حل آن حاصل میشود.
در واقع معادله شرودینگر بر اساس فرض موج بودن الکترون(در نتیجه در نظر گرفتن تابع موج برای آن) و با استفاده از رابطه دوبروی نوشته میشود. استفاده از رابطه دوبروی و موج فرض کردن الکترون نکته اساسی معادله شرودینگر است. شرودینگر با این فرضهای مهم و با انجام محاسبات ریاضی پیچیده به نتایج قابل توجهی در احتمال توزیع الکترون در یک فضا و همینطور مقادیر مجاز برای انرژی الکترون دست یافت.
ورودیهای معدله شرودینگر عبارتند از انرژی پتانسیل و شرایط مرزی. انرژی پتانسیل بیان میکند که در محیط مورد بررسی چه نیروهایی به الکترون وارد میشود و شرایط مرزی بیان میکند که الکترون در چه مکانی و با چه هندسهای قرار دارد. خروجیهای ارزشمند این معادله نیز عبارتند از انرژیهای مجاز برای الکترون و همینطور احتمال توزیع الکترون. انرژیهای مجاز بیان میکنند که الکترون چه مقادیری از انرژی را در آن فضا میتواند داشته باشد و احتمال توزیع نیز بیان میکند که در چه فضاهایی احتمال حضور الکترون بالاست (مثالهای آن در ادامه برای فهم بهتر در چند خاص آورده شده است).
شکل کلی تابع موج (معادله۲) و همینطور معادله شرودینگر (معادله۳) مستقل از زمان در زیر آورده شده است:
|
معادله۲ |
|
|
معادله۳ |
برای مثال چند حالت طبق معادله شرودینگر بررسی میشود. قابل ذکر است که در اینجا هدف حل معادله شرودینگر نیست و نتیحه و تحلیل آن مدنظر است.
۱-۳- الکترون آزاد
منظور از الکترون آزاد در اینجا، الکترونی است که میتواند هرجایی از فضا قرار بگیرد و هیچ محدودیت فضایی ندارد. همچنین انرژی پتانسیل نیز در تمام فضا صفر گرفته میشود و عملا فرض میشود که در هیچ جایی از فضا نیرویی به آن وارد نمیشود. در واقع این حالت سادهترین شرایطی است که میتواند برای الکترون پیش بیاید. معادله شرودینگر این حالت برابر است با:
|
معادله۴ |
دو نتیجهای که با حل این معادله به دست میآید، یکی اینکه احتمال توزیع الکترون یک عدد ثابت است، یعنی برای الکترون فرقی نمیکند که در چه جایی از فضا قرار بگیرد و عملا الکترون هرجایی از فضای بینهایت میتواند باشد. نتیجه دوم نیز این است که گسستگی در مقادیر انرژی الکترون وجود ندارد و عملا انرژی آن با شرایط مذکور پیوسته است.
۲-۳- الکترون محدود در یک بعد
در این حالت فرض میشود که الکترون در یک فضای یک بعدی گیر افتاده است. این حالت در شکل۱ نمایش داده شده است.
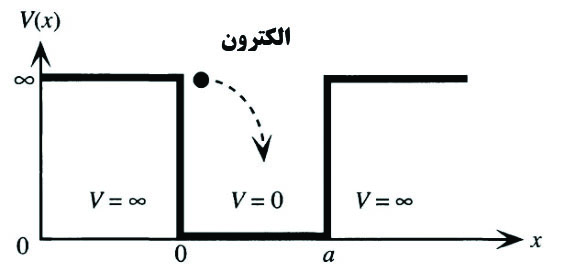
شکل۱- الکترون محدود در یک بعد[۱]
مطابق شکل۱ دیده میشود که عملا الکترون در یک فضای یک بعدی با اندازه a گیر افتاده است، چراکه در این فضا پتانسیل صفر است ولی خارج از آن پتانسیل بینهایت است.
با حل معادله شرودینگر در این حالت نتایج جذابی به دست میآید. اولا مشاهده میشود که به محض محدود شدن الکترون در یک فضا، گسسته شدن مقادیر انرژی برای آن اتفاق میافتد. مقادیر انرژی مجاز الکترون در این حالت در معادله۵ آورده شده است:
|
معادله۵ |
در این معادله n یک عدد صحیح است. h ثابت پلانک، a طول ناحیه نشان داده شده در شکل۱ و m جرم الکترون است. مطابق این معادله دیده میشود باتوجه به اینکه n چه عددی باشد، الکترون صرفا مقادیر خاصی از انرژی را میتواند دارا باشد.
مقادیر انرژی مجاز به صورت شماتیک و همچنین احتمال توزیع الکترون در این حالت در شکل۲ نمایش داده شده است.
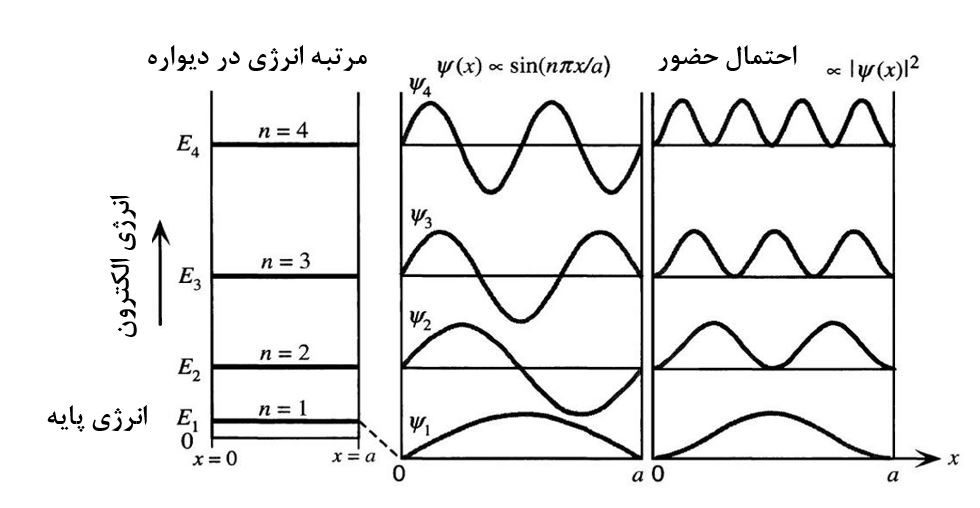
شکل ۲- انرژیهای مجاز الکترون و همچنین احتمال توزیع الکترون در حالت الکترون محدود در یک بعد[۱]
مطابق شکل۲ مشاهده میشود که با توجه به اینکه الکترون چه انرژی داشته باشد، احتمال توزیع آن در محدوده ۰ تا a متفاوت است. اگر انرژی الکترون در حالت پایه باشد (n=۱) همانطور که نشان داده شده است احتمال حضور الکترون در فضای وسط a/۲ ماکزیمم است. اما اگر انرژی الکترون در حالت ثانویه باشد یعنی n=۲ باشد، احتمال حضور الکترون در a/۲ برابر صفر است و الکترونها با احتمال بیشتر در a/۴ یا ۳a/۴ قرار دارند. برای مقادیر دیگر نیز در شکل نشان داده شده است. این نتایج نشان میدهد که چقدر نتایج حاصل از معادلات شرودینگر میتوانند مفید باشند چراکه از لحاظ تئوری نمیتوان توضیح داد که چرا تغییر n از ۱ به ۲ باعث این میشود که حضور الکترون در آن فضا اینقدر تغییر کند و فهمیدن آن تنها وابسته به حل معادلات شرودینگر و استفاده از نتایج آن است [۱].
۳-۳- الکترون محدود در سه بعد
با گسترش حالت قبل از یکبعد به سهبعد میتوان حالتهای واقعیتر مثل قرار گرفتن الکترون در یک اتم را بررسی نمود. در این حالت عملا الکترون در یک جعبه سهبعدی گیر افتاده است که در شکل۳ نمایش داده شده است.
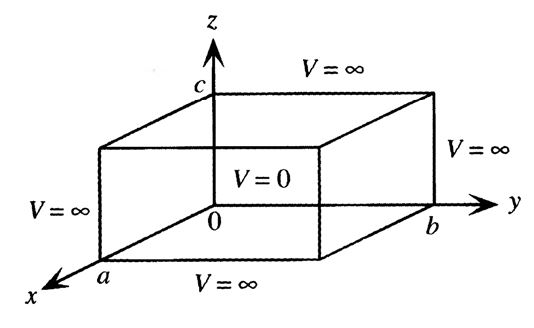
شکل ۳- نمایش محل قرارگیری الکترون در حالت الکترون محبوس در سهبعد و پتانسیلهای موجود[۱]
مطابق این شکل مشاهده میشود که الکترون درون جعبه با ابعادی a×b×c قرار دارد که در آن پتانسیل صفر است و خارج از آن پتانسیل بی نهایت است.
در این حالت نیز در صورت حل معادله شرودینگر، گسستگی در مقادیر انرژی الکترون مشاهده میشود که مطابق معادله۶ است:
|
معادله۶ |
در این حالت انرژی به سه عدد طبیعی بستگی دارد. اما برای مطالعه دقیقتر الکترون در شرایط واقعی مثل الکترون موجود در یک اتم نیاز است تا به جای مختصات کارتزین (مثل نمونه بالا) از مختصات کروی استفاده شود. این مورد در بخش بعد آورده شده است [۱].
۴-۳- الکترون محدود در یک اتم
این حالت مشابه بخش قبل است منتها به جای مختصات دکارتی از مختصات کروی استفاده میشود تا دقیقا وضعیت الکترون در یک اتم بررسی شود. نتیجه حل معادله شرودینگر در این حالت در شکل۴ نشان داده شده است.
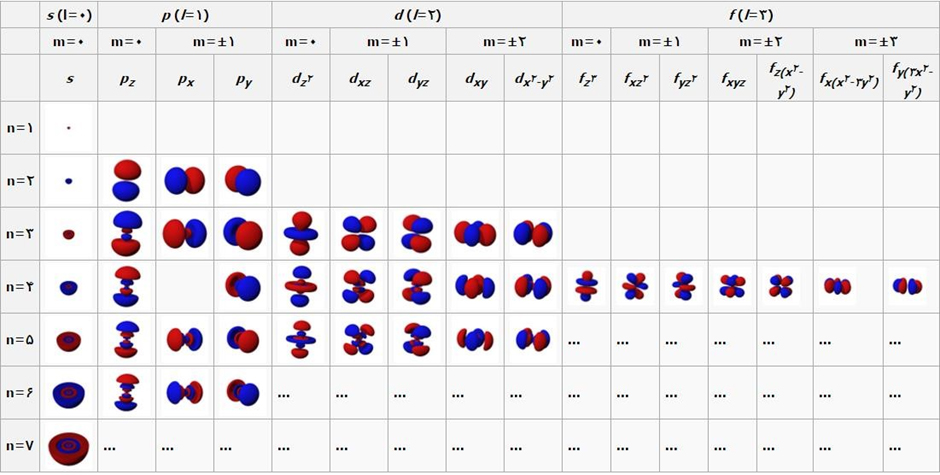
شکل ۴- حل معادله شرودینگر در سهبعد و در مختصات کروی و نمایش اوربیتالها[۲]
در این حالت مشابه شکل۴، احتمال حضور الکترون توسط سه عدد کوانتومی اصلی n، l و ml نمایش داده میشود. برای مثال در حالتیکه n=۱ باشد تنها اوربیتال s با l=۰ میتواند حضور داشته باشد که شکلی کروی دارد. یعنی در حالت پایه انرژی الکترون، الکترون در یک فضای کروی اطراف هسته با یک شعاع معین میتواند حضور داشته باشد که به آن اوربیتال ۱s گفته میشود. منظور از اوربیتال فضایی است که الکترون به احتمال ۹۵% درون آن قرار دارد. در صورتیکه انرژی الکترون مقادیر بالاتری را پیدا کند در اوربیتالهایی با شکل و شعاعهای دیگر هم میتواند قرار گیرد. برای مثال میتوان به اوربیتال دمبلی شکل ۲p اشاره کرد. سایر اشکال اوربیتالها نیز که نشانگر احتمال حضور الکترون در یک فضای اطراف هسته هستند، در شکل۴ نشان داده شده است.
همچنین قابل ذکر است که موارد دیگری همچون تونل زنی الکترون، حضور الکترون در یک شبکه کریستالی و موارد متعدد دیگر را نیز با معادله شرودینگر میتوان بررسی نمود و در هر یک مقادیر دقیق مجاز انرژی و احتمال توزیع الکترون را بدست آورد که به علت پیچیدگی در اینجا ذکر نمیشود [۱].
۴- اصل عدم قطعیت هایزنبرگ
یکی از اصول مورد استفاده در فیزیک کوانتوم، اصل عدم قطعیت هایزنبرگ است که در واقع به دوگانگی موجی-ذرهای اجسام وابسته است. این اصل به صورت ساده بیان میکند که امکان تعیین دقیق سرعت و مکان با خطای صفر وجود ندارد. البته در اینجا نیز باید گفت که درست است که این اصل عام هست منتها برای اجسام بزرگ به قدری ناچیز است که درنظر گرفته نمیشود و با مواردی همچون الکترون در یک اتم است که قابل توجه است و باید آن را در نظر گرفت. دو شکل معروف از این اصل در زیر نشان داده شده است (از اولی میتوان دومی را بدست آورد).
|
معادله۷ |
|
|
معادله۸ |
در واقع این اصل نشان میدهد که همواره در تعیین مکان و همینطور سرعت (به بیانی تکانه) مقداری خطا وجود دارد که حاصلضرب آنها بزرگتر مساوی مقداری در حدود ۳۴-۱۰ ژول است. عملا مطابق این اصل بیان میشود که در صورتیکه مکان دقیق یک الکترون گزارش شود (یعنی به سمت صفر برود) باتوجه به این معادله p∆ به سمت بینهایت میل میکند و عملا دیگر هیچ حرفی از سرعت الکترون نمیتوان زد و همچنین برعکس. دلیل آن نیز این است که برای فهمیدن مکان دقیق الکترون برای مثال باید الکترون دیگری به آن شلیک کرد تا با برگشت آن مشخص شود مکان دقیق الکترون کجا بوده است. در اثر برخورد دو الکترون ولی سرعت الکترون تغییر میکند و دیگر در مورد سرعت آن چیزی نمیتوان گفت.
همچنین طبق معادله دوم، رابطه بازه انرژی و بازه زمان نشان داده شده است که همواره حاصلضرب آنها نیز بزرگتر مساوی مقدار ۳۴-۱۰ ژول است. یعنی در صورتیکه انرژی یک الکترون یکبار اندازهگیری شود، در صورتیکه یک آنگستروم ثانیه بعد مجددا اندازهگیری شود، حداقل انرژی گزارش شده با انرژی اولیه ۲۴-۱۰ ژول تفاوت دارد.
همانطور که بیان شد، اصل عدم قطعیت هایزنبرگ برای مثال برای یک توپ نیز صادق است ولی باتوجه به اینکه مقادیر انرژی با مرتبه بزرگی ۳۴- ژول برای توپ ناچیز است عملا از آن صرف نظر میشود [۱-۳].
در ادامه به تعدادی از نتایج اصل عدم قطعیت هایزنبرگ اشاره میشود:
۱-۴- طیف عبوری الکترونی از شکافی باریک
مشاهده شده است که اگر طیفی از الکترونها از یک شکاف عبور کنند و به دیواری که پشت آن قرار دارد بخورند ، با باریکتر کردن شکاف به مرور پهنا باریکه برخوردی الکترون به دیوار نیز باریکتر میشود. منتها وقتی اندازه شکاف بسیار باریک شود، در کمال ناباوری پهنای باریکه برخوردی به دیوار ناگهان بزرگ میشود. این حالت در شکل۵ نشان داده شده است.
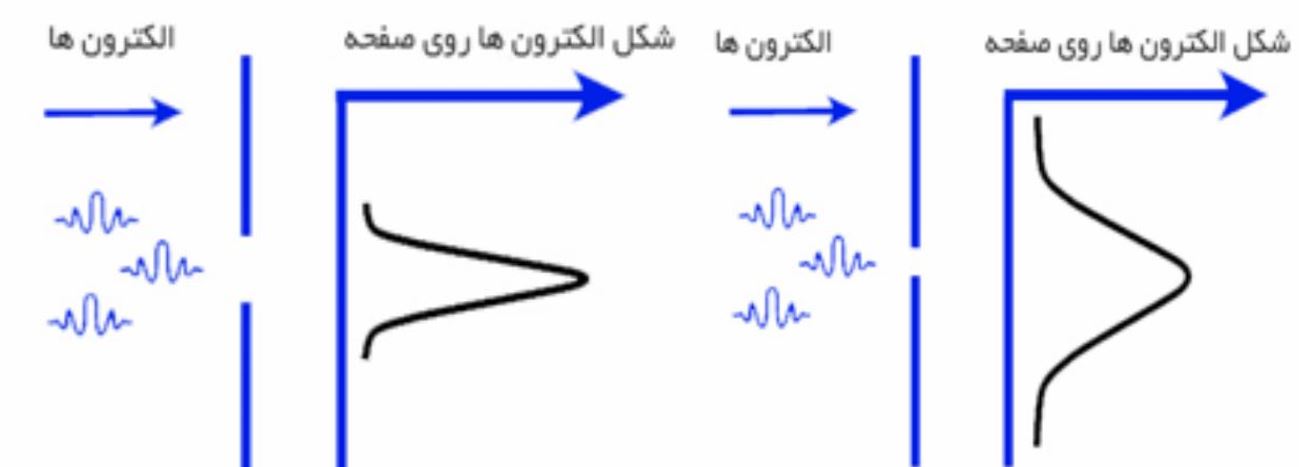
شکل ۵- گستردهتر شدن بازه برخوردی الکترون عبور کننده از یک شکاف باریک در اثر اصل عدم قطعیت هایزنبرگ
دلیل این امر این است که وقتی شکاف بسیار باریک میشود، مکان عبوری الکترونها دقیقتر میشود و عملا x∆ کاهش مییابد. مطابق اصل عدم قطعیت هایزنبرگ با کاهش باید افزایش یابد. افزایش آن یعنی افزایش بازه سرعت و افزایش بازه سرعت نیز باتوجه به برداری بودن سرعت یعنی پهنتر شدن بردار سرعت و پهن شدن باریکه برخوردی الکترون عبوری از شکاف به دیوار پشتی.
۲-۴- عدم سقوط الکترون بر روی هسته
مطابق اصل عدم قطعیت هایزنبرگ عملا هیچگاه الکترون نمیتواند برروی هسته سقوط کند چراکه در این صورت مکان آن دقیقا مشخص میشود (روی هسته قرار میگیرد) و همچنین سرعت آن نیز دقیقا مشخص (برابر صفر) میشود. با توجه به اصل عدم قطعیت هایزنبرگ این حالت ممکن نیست و در نتیجه الکترون بر روی هسته نمیتواند سقوط کند.
۳-۴- رسیدن به صفر کلوین
مشابه توضیحات در بخش قبل، عملا رسیدن به صفر کلوین و صفر شدن سرعت و همینطور ثابت شدن مکان بدون هیچگونه نوسانی ممکن نیست.
همچنین موارد دیگری نیز طبق اصل عدم قطعیت هایزنبرگ قابل توضیح هستند که دلایل مشابه مطالب گفته شده دارد. از جمله آنها میتوان به پهنشدگی خطوط طیفی یا انرژی نقطه صفر اشاره کرد.
۵- جمعبندی و نتیجهگیری
همانطور که در این مقاله بیان شد، خاصیت دوگانگی موجی-ذرهای و همینطور گسسته بودن انرژی عام است و برای همه اجسام صدق میکند. اما این حالت برای اجسام بزرگتر ملموس نیست و برای ذراتی همچون الکترون ملموس است و اثرات آن دیده میشود. این توضیحات برای مشاهده اصل عدم قطعیت هایزنبرگ نیز صادق است. از مهمترین نتایجی که توسط فیزیک کوانتوم گرفته میشود، حل معادله شرودینگر برای الکترون در شرایط مختلف است که یکی از مهمترین آنها مربوط به الکترون درون یک اتم است. با حل معادله شرودینگر در این حالت سه عدد کوانتومی اصلی بدست میآید و باتوجه به آن میتوان اوربیتالهای مرجح الکترون در یک اتم را تعیین نمود.
۶- مراجع
[1]. Kasap, Safa O. Principles of electronic materials and devices. Vol. 2. New York: McGraw-Hill, 2006.
[2]. Mitin, Vladimir V., Dmitry I. Sementsov, and Nizami Z. Vagidov. Quantum mechanics for nanostructures. Cambridge University Press, 2010.
[3]. Levi, Anthony Frederic John. Applied quantum mechanics. Cambridge University Press, 2006.